电磁层析成像下的石油勘探论文
2020-09-23 07:47:55 97
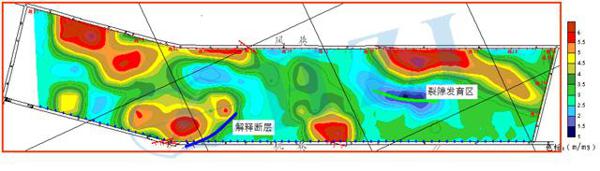
1石油勘探中的电磁层析成像原理
在石油勘探过程中,需要准确分析不同岩层的准确声层析成像声波,将分析结果用作石油勘探图像重建的主要基础。重建结果的好坏直接影响到后续工作:详细原理如下:
1)对石油勘探中所有电磁层析成像信号进行信号分解,信号波变换值x(n, P)。
2)通过操作获得电磁层析成像信号的分解尺度S(n,p)。可以根据以下公式计算上述成像信号分解结果的相关性:
3)对于所有电磁层析成像信号分解结果的归一化变换可如下获得PS(n,p)= S(n,p)Qx(n)Qs(n),q = 1,2,...,q(1)在上式中,Qx(n)= ∑px(n,p)2QS(n) = ∑pS(n,p)2
4)PS(n,p)和x比较(n,p)的绝对值。假设ps(n,p)|| x(n,p)|,可以确定此位置的信号转换值与初始电磁层析成像信号是分开的。此时,需要将x(n,p)分配给xg(n,p),并且将S(n,p)同时设置为零。否则,需要保留x(n,p)的初始值。
5)根据以上解释,我们可以知道x(n,p)是由电磁层析成像信号中的声波引起的,则Qx(n)/(M-1)是信号变换在一定尺度上估计声波均方误差的结果。可以使用以下公式计算声波无偏估计结果μ= Qx(n)/(M-1)ζn(2)将上述无偏估计结果与阈值进行比较。如果大于阈值,则返回到步骤(2),然后继续,否则,结束迭代过程。 6)根据xg(n,p)对电磁体层摄影信号的声波进行逆信号变换处理。假设μ> 1,可以得到sin(μ-1)> 0,并且假设μ1,则可以得到sin(μ-1)0。根据上述特征,可以得到最佳的估计结果,如下所示:d→d + sin [β(μ-1)](3)在上述公式中,β可用于描述电磁波的步长石油勘探中的层析成像信号。调整因子。在第一次迭代过程中,d的值设置为1,如果使用μ1,则可获得sin(μ-1)0。上式可以用于迭代处理,并且d的值可以连续减小。将该值乘以相应的相关系数,以减少所采样的数量,直到μ的值接近1。假设μ> 1,我们可以知道sin(μ-1)> 0,然后根据上式进行迭代处理。 d的值将继续增加。将该值乘以相关系数可以增加样本数量。减小声波滤波误差,直到μ的值接近1。从上面的描述可以知道,如果对石油勘探电磁层析成像中的复杂结构进行声波滤波,则信号系数的方差和声波的方差相等,可以获得理想的声波滤波效果。 。在滤波过程中,为了保证声波滤波过程的稳定性,提高滤波过程中的收敛速度,有必要在滤波过程中引入调整因子。假设调整因子的值较大,则收敛速度大大提高。但是,过滤效果相对较差。另一方面,尽管会降低收敛速度,但是滤波效果更好。根据以上内容,可得调整因子的计算公式如下:ζn2=ζ2×‖i0* i1 *…* ik-2 * hk-1‖ 2(4)根据上述方法,电磁可以得到层析层析声波滤波的时间调整因子,完成声波滤波,获得高质量的成像信号,实现石油勘探中的电磁层析层析声波滤波。但是,通过声波勘探石油岩层来形成稳定的图像一直存在问题。石油区的岩层结构复杂。电磁层析成像技术将在复杂的岩石结构中产生声像变化并形成图像干扰。传统的电磁层析成像在石油勘探的这种干扰之下,普通的电磁层析成像会造成干扰损失并影响成像效果。
2成像信号的声波滤波优化方法理论
使用传统算法在石油勘探电磁层析成像中进行声波滤波,假设岩石的形成探测目标太复杂,会引起大量声波掺杂到成像信号中,对成像信号造成干扰。为此,提出了一种基于加权小波分析算法的石油勘探电磁层析成像中复杂结构的声波滤波方法。
2.1计算成像信号的权重
对于在石油勘探过程中收集的电磁层析成像信号,可以得到如下相应的非线性方程:yl = gl(yl-1,Xl-1 )zl = il(yl,wl {)(5)在上式中,wl可用于描述电磁层析成像信号的概率密度函数。过滤成像信号中的声波的详细过程如下
1)初始化成像信号。当l = 0时,有必要使样本符合yj0〜Q(y0)分布。
2)当l = 1、2,...,U时,需要选择一组成像信号作为样本。
3)根据随机向量计算相应的权重。随机向量为wj,j = 1,2,...,P。4)使用以下公式更新电磁层析成像信号:p(yl | Zl)≈∑Pj =1wjlε(yl-yjl)j = 1 ,2,...,P(6)是狄拉克函数。
2.2成像信号的重构
在这一阶段,小波分析方法已应用于各个行业,并发挥着越来越重要的作用。加权法与小波分析法相结合即可完成像信号声波一样过滤。可以使用以下公式执行小波变换处理:XUg(b,c)= 1 | b | ∫-g(y)ζ*(y)dy = g,ζb,{}cζb,c(y)= 1 | b | ζ(y-cb)b,c∈S,b≠{0(7)在上式中,ζb,c(y)可用于描述小波母函数,b可用于描述尺度变换算子,和c可用于描述成像信号采样时间。石油勘探中电磁层析成像信号的时间与相应位置密切相关。 ζ*(u)可用于描述ζ(u)的共轭函数。以下公式可用于对石油勘探2k2ζ(2ky-1)(8)中的电磁层析成像信号执行离散变换处理,即:b = 12kc = l2 {k分解处理dk,l = ∑ni(n-2l )dk-1,nek,l =Σnh(n-2l)dk-1,{n(9)其中n = 0,1,2,...,P -1。以下公式可用于重建所有成像信号分解因子:dk,n = ∑ldk + 1,li(n-2l)+Σlek+ 1,lh(n-2l)(10)可以使用所描述的方法过滤成像信号的声波信号,在石油勘探中获得清晰的电磁层析成像信号。
3实验结果分析
为了验证基于加权小波分析算法的石油勘探中电磁层析成像复杂结构的声波滤波方法的有效性,需要一个实验。在实验过程中,根据岩层回波的电磁信号,收集了电磁成像信号。使用用于电磁层析成像信息获取的传统算法,所获得的信号成像获取结果可以在图5中表示。使用改进的算法对成像信号进行声学滤波,可以在图2中表示获得的成像信息收集结果。 3.根据上述两帧图像,可以知道,通过使用改进的算法对成像信号进行声信号滤波,得到的结果更接近实际情况,大大提高了图像的真实性。成像信号的滤波结果。通过对以上实验数据进行整理和分析,可以得出不同算法得到的成像信号真实性的比较结果:根据以上两张表中的数据,可以知道,改进算法用于在石油勘探中执行电磁层析成像信号的声学过滤。 ,这大大提高了成像信号的真实性,并降低了成像信号中的信噪比。
4结论
针对由于传统算法无法避免的,由于勘探目标岩石地层复杂而导致成像信号受干扰的缺陷,提出了一种加权小波分析算法,用于石油勘探。电磁层析成像中复杂结构的声学滤波方法非线性方程式用于描述所有石油勘探中电磁层析成像结构的声波。选择一组成像信号作为样本数据,计算成像信号的权重,并获得所有成像信号在声波滤波过程中的重要性。对以上结果执行小波变换处理以完成成像信号的分解重建了所有因素,以实现声学滤波。实验结果表明,将改进算法用于石油勘探电磁层析成像的声学结构滤波,可以大大提高成像信号的真实性,降低信号的信噪比,满足石油勘探的实际需求。










